Contents
- 1 All phonemes
- 2 Vowels & consonants
- 3 Place & manner of articulation
- 4 Bigrams and entropy
- 5 Sources
Introduction
This is a statistical evaluation of the Sindarin dictionary hosted at http://www.sindarin.de.
1 All phonemes
The frequencies of all Sindarin phonemes are found to be:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Notation (for easiness of counting, digraphs were converted to unigraphs):
- k for /k/, pronounced [k], spelled <c> by Tolkien
- þ for /þ/, pronounced [þ], spelled <th> and sometimes <þ> by Tolkien
- ð for /ð/, pronounced [ð], spelled <dh> and sometimes <ð> by Tolkien
- χ for /x/, pronounced [x] or [χ], spelled <ch> by Tolkien
- j for /j/, pronounced [j], spelled <i> by Tolkien
- R for /r̥/, pronounced [r̥], spelled <rh> by Tolkien
- L for /ɬ/, pronounced [ɬ], spelled <lh> by Tolkien
- W for /ʍ/, pronounced [ʍ], spelled <hw> or <wh> by Tolkien
Assumptions for simplicity:
- The difference between long and short vowels is neglected.
- Diphthongs are counted as two vowels.
- It is not always clear how <ng> is supposed to be pronounced (either /ŋ/ or /ŋg/). It was treated as /n/ + /g/.
1.1 Discussion
For the rank-frequency distribution p(r) (where r is a phoneme’s rank), an ad-hoc formula was first proposed by Zipf in 1929 [1]:
| p(r) ∼ |
|
with the normalization s(N)=∑k=1N 1/k, where N is the total amount of phonemes.
Several authors noticed since then that it does not fit the data across languages too well and have proposed other ad-hoc fitting functions [3, 4]. In 1988, Gusein-Zade proposed a formula [2] based on a sensible assumption, namely that rank-frequencies are drawn from a uniform probability density and that p(r) can be approximated by the corresponding expectation value for any given language. This leads to:
| p(r) = |
|
|
|
For large N and for large r at fixed N this can be approximated by:
| p(r) ≈ |
| log |
|
It turns out that this formula describes real-language data rather well and no wild fitting is required (see below). The fact that a model assumption enters the calculation seems to have been overlooked or misunderstood by other authors, probably because Gusein-Zade’s paper was published in Russian. One can see that it makes no sense to generalize the Zipf distribution by adding fittable parameters, like r−β (as it often seems to be done) because the dependency is different, approximately log1/r rather than a power law1. This means that a semilogarithmic plot of p(r) should produce a straight line. This is indeed the case for the Sindarin data, as seen in fig. 1.
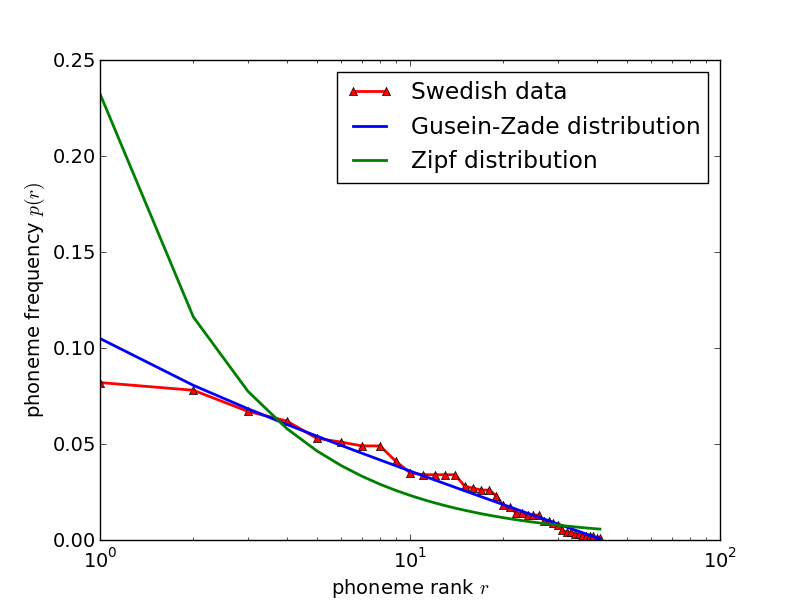
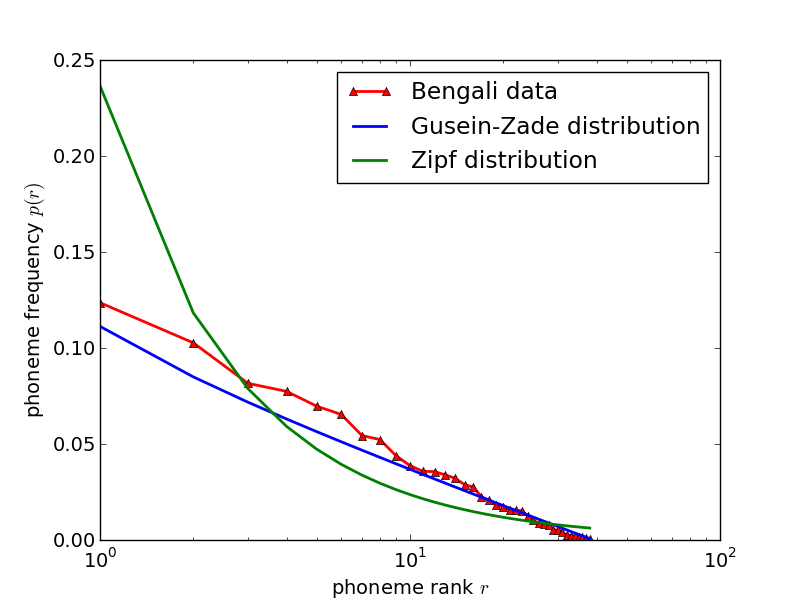
Comparing it with data from natural languages (fig. 2) one finds a similarly good agreement for English and Swedish, somewhat worse for Bengali. Except for Bengali, deviations are spread both above and below the Gusein-Zade function which suggests a statistical rather than a systematic error. I do not know how reliable the Bengali data are.
Note that the formula does not predict how common a certain sound is, but rather how frequent the phoneme ranked r is (whatever the phoneme itself may be). It turns out that this value is completely determined by the total amount of phonemes N.
Note also that it matters for the individual frequencies whether one considers a dictionary or a text. In the latter case, English [ð] obviously becomes much more common [5] due to the thes and thats (in Sindarin texts, the frequency of i is expected to go up for the same reason). However, the distribution seems to stay the same: The RP data in figure 2 are from a dictionary, the American English data from a text.
Finally one should note that the RP data for English include diphthongs as separate phonemes, while the American English data do not; but again, this does not seem to affect the distribution itself.
We can thus conclude that the rank-frequency distribution of the Sindarin phonemes is indistinguishable from that of a natural language.
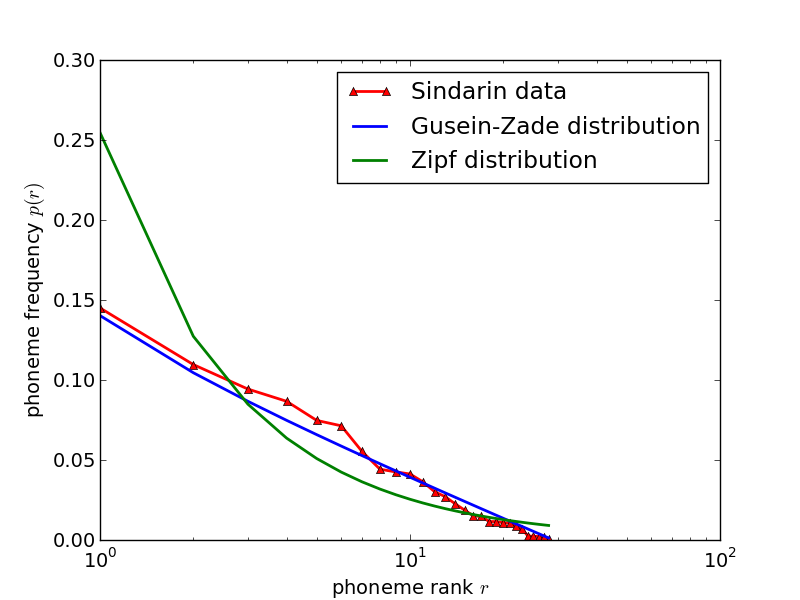
Figure 1: Rank-frequency distribution of Sindarin phonemes
Figure 2: Rank-frequency distributions of phonemes for various natural languages. The American English, Swedish and Bengali data are from the references in [3], the RP data are from [5].
2 Vowels & consonants
Rank frequencies for vowels only:
| ||||||||||||||||||||||||
Rank frequencies for consonants only:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Vowel-to-consonant ratio:
|
3 Place & manner of articulation
Place of articulation:
|
Manner of articulation:
|
Distribution among stops:
| ||||||||||||||||||||||||
Distribution among fricatives:
| |||||||||||||||||||||||||||
Distribution among sonorants/semivowels:
| |||||||||||||||||||||||||||||||||
4 Bigrams and entropy
A bigram is a cluster of two letters, or, in this case, two phonemes. One can introduce the conditional probability pi(j) to find the phoneme j if the preceding phoneme is i. It forms a matrix with normalized rows: ∑j pi(j) = 1. If one weighs the rows with the frequencies p(i), one obtains the probability to get the phonemes i and j in two sequential draws: p(i,j) = p(i)pi(j). This is now of course normalized with respect to the total sum: ∑ij p(i,j) = 1. The procedure is readily generalized to n-grams.
Linguistically, the matrix shows us a language’s phonotacics and the restriciveness of its phonology. (Probably, one can also use it to write a ruthlessly efficient hangman algorithm.) Obviously, the higher the spread of values across the bigram matrix, the freer the phonology. This is exactly what is measured by the n-gram entropy2:
| Hn = − |
| p(i1,i2,…,in) log2(p(i1,i2,…,in)) |
Hn can already be computed for the unigram frequencies p(i), but as discussed above, their distribution is mostly determined by the total amount of phonemes N, so that the same goes for the entropy. It seems more interesting to look at the bigram entropy H2: The smaller it is, the more restrictive the phonology. Note that for any value of n, Hn has the maximum value of Hmax=log2(N) which corresponds to the case that all n-grams are equiprobable, which would make the phonology absolutely free and all the phonemes uncorrelated.
The following three tables show pi(j), computed for vowels only, consonants only, and for all phonemes. Colors are used as a visual guide to highlight values from 0.1 to 0.2 (blue); 0.2 to 0.3 (green); 0.3 to 0.4 (purple); 0.4 to 0.5 (orange); and finally above 0.5 (red).
Vowels only:
|
Consonants only:
|
All phonemes:
|
For the unigram and bigram entropies, one obtains:
| ||||||||||||||||||
Unfortunately, data from natural languages are hard to come by. For English, Shannon gives H1=4.14, H1/Hmax=0.88 and H2=3.56, H2/Hmax=0.76. However, this was calculated for the N=26 Latin letters rather than for phonemes. Making a comparison nevertheless, one can see that the phonology of Sindarin is much more restricted, which makes sense.
H2 is expected to be smaller than H1 for any language (which is equivalent to the existence of phonotactics). To find a lower bound, languages like Japanese or Hawaiian are promising candidates.
5 Sources
To get a distribution by source, only unique entries were counted. Because of the ubiquitous conceptual changes by Tolkien, an editorial decision has to be made regarding what to count as unique.
For example, N. naith ’gore’ (Ety:387), S. neith, naith ’angle’ (PE17:55) and S. naith ’spearhead, gore, wedge, narrow promontory’ (UT:282) were regarded as the same (polysemous) word, with various possible translations into English, and a joined reference (Ety:387, PE17:55, UT:282).
On the other hand, S. eitha- ’1. prick with a sharp point, stab 2. treat with scorn, insult’ (HEK-, WJ:365) and S. eitha- ’to ease, assist’ (ATHA-, PE17:148) are clearly two different (homophonous) words, and are therefore kept separate. In this case it is obvious from their different etymologies.
There is a grey zone, however: For example, EN baran ’brown, swart, dark-brown’ and S. baran ’brown, yellow-brown’ suggest a conceptual change, albeit a small one, so that they were counted as separate entries, and thus also as different words for the statistics.
This gives the following absolute and relative counts (compare also the Hiswelóke charts [8]):
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Of course, a good amount of words is attested in various sources, so that the added count is higher than the actual entry count. The Venn diagram in figure 3 shows how words are shared across the two top sources (The Etymologies and Parma Eldalamberon 17) and the rest.
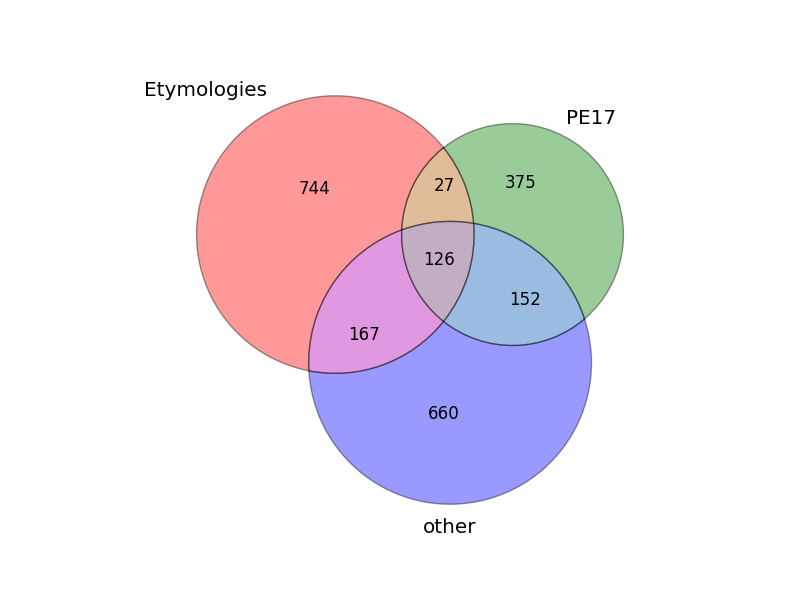
Figure 3: Sindarin vocabulary sources
References
- [1]
- G. K. Zipf, Relative frequency as a determinant of phonetic change, Harvard studies in classical philology, Vol. 40 (1929), pp. 1-95
- [2]
- С. М. Гусейн-Заде, О распределении букв русского языка по частоте встречаемости, Пробл. передачи информ. 24:4 (1988), 102–107
- [3]
- B. Sigurd, Rank-frequency distributions for phonemes, Phonetica 18: 1-15 (1968)
- [4]
- W. Li, P. Miramontes, G. Cocho, Fitting ranked linguistic data with two-parameter functions, Entropy 2010, 12, 1743-1764
- [5]
- J. Higgins, RP phonemes in the Advanced Learner’s Dictionary, http://myweb.tiscali.co.uk/wordscape/wordlist/phonfreq.html
- [6]
- C. E. Shannon, A mathematical theory of communication, The Bell system technical journal, 27, 379-423, 623-656 (1948)
- [7]
- C. E. Shannon, Prediction and entropy of printed English, The Bell system technical journal, 30(1), 50-64 (1950)
- [8]
- Hiswelóke Sindarin dictionary statistical charts http://www.jrrvf.com/hisweloke/sindar/online/sindar/charts-sd-en.html
- 1
- This does not mean that the Zipf distribution cannot be applicable somewhere else. It does seem to describe the distribution of words in a text [7].
- 2
- The logarithm to base 2 is a convention and one says then that the entropy is measured in ”bits”. Of course, this sets the scale rather than the unit – H is dimensionless.
The interpretation of H in information theory is as (the average) uncertainty: H is zero if a probability is equal to one (a completely certain event), increases with N (the more outcomes, the higher the uncertainty), and is maximal at fixed N if all probabilities are equal (all outcomes equiprobable, hence maximal uncertainty). Finally, the uncertainty of two independent events is the sum of the individual uncertainties.
This document was translated from LATEX by HEVEA.
.png)
.png)